Önerme Nedir, Bir Önermenin Olumsuzu (Değili) konu anlatımı soruları çözümleri 9. sınıf

Doğru yada yanlış olarak kesin hüküm bildiren ifadelere önerme denir. Önermeler genellikle p, q, r, s, t gibi küçük harflerle gösterilir. Bir önermenin doğru ya da yanlış olmasına o önermenin doğruluk değeri denir. Bir önerme doğruysa doğruluk değeri “1” ile yanlış ise doğruluk değeri “0” ile gösterilir. Örneğin p önermesi doğruysa p ≡ 1, yanlışsa p ≡ 0 şeklinde gösterilir.

Örnek: Aşağıdaki ifadelerin hangilerinin önerme olduğunu bulalım.
a) Türkiye’de yüz ölçümü en büyük olan şehir İstanbul’dur.
b) 7 + 8 = 15
c) 12 – 3 < 8
ç) Bana yardım edecek misin?
d) Bugün alış verişe gidelim.
e) Bugün hava çok sıcak.
f) Dersine iyi çalış.
g) Keşke, biraz daha erken gelseydim.
h) İki tek sayının toplamı çift sayıdır.
i) x + 5 = 11

Çözüm: a) “Türkiye’de yüz ölçümü en büyük olan şehir İstanbul’dur.” ifadesi kesin bir hüküm bildirdiği için önermedir.
b) “7 + 8 = 15” kesin bir hüküm bildirdiği için önermedir.
c) “12 – 3 < 8” kesin bir hüküm bildirdiği için önermedir.
ç) “Bana yardım edecek misin?” ifadesi bir soru ifadesidir. Doğru ya da yanlış kesin bir hüküm bildirmediği için önerme değildir.
d) “Bugün alış verişe gidelim.” ifadesi istek bildirir. Doğru ya da yanlış kesin bir hüküm bildirmediği için önerme değildir.
e) “Bugün hava çok sıcak.” ifadesi bir durum bildirir ve görecelidir. Doğru ya da yanlış kesin bir hüküm bildirmediği için önerme değildir.
f) “Dersine iyi çalış.” ifadesi emir bildirir. Doğru ya da yanlış kesin bir hüküm bildirmediği için önerme değildir.
g) “Keşke, biraz daha erken gelseydim.” ifadesi pişmanlık bildirir. Doğru ya da yanlış kesin bir hüküm bildirmediği için önerme değildir.
h) “İki tek sayının toplamı çift sayıdır.” ifadesi kesin bir hüküm bildirdiği için önermedir.
i) “x + 5 = 11” ifadesi kesin hüküm bildirdiği için önermedir. (Bu önerme açık önerme olup niceleyiciler konusunda ayrıntılı olarak anlatılacaktır.)

Örnek: Aşağıdaki önermelerin doğruluk değerini bulalım.
a) p: “Üçgenin iç açılarının ölçüleri toplamı 180⁰ dir.”
b) q: “Bütün asal sayılar tek sayıdır.”
c) r: “√5 bir rasyonel sayıdır.”
ç) t: “|-6 + 2| < |-6| + |2|

Çözüm: a) p: önermesinin doğruluk değeri 1 dir. Çünkü üçgenin iç açılarının ölçüleri toplamı 180⁰ dir.
b) q önermesinin doğruluk değeri 0 dır. Çünkü “bütün asal sayılar tek sayıdır” ifadesi yanlış bir önermedir.
c) r önermesinin doğruluk değeri 0 dır. Çünkü √5 sayısı rasyonel değil, irrasyonel sayıdır.
ç) t önermesinin doğruluk değeri 1 dir. Çünkü |-6 + 2| < |-6| + |2|
yani 4 < 6 + 2 dir.

İki Önermenin Denkliği

Doğruluk değeri aynı olan önermelere denk önermeler denir. p ve q önermeleri denk ise bu durum p ≡ q biçiminde gösterilir ve “p denktir q” diye okunur. p önermesi q önermesine denk değilse

$p ≢ q$

biçiminde gösterilir.

Örnek: Aşağıdaki önermelerden denk olanları belirtelim.
a) p: “91 sayısı asal değildir.”
b) q: “İstanbul Türkiye’nin başkentidir.”
c) r: “x = 5 ise x + 7 = 12 dir.”
d) t: “En küçük negatif tam sayı -1 dir.”

Çözüm: a) 91 = 13.7 olduğundan “91 sayısı asal değildir.” Dolayısıyla p önermesinin doğruluk değeri 1 dir. Yani p ≡ 1 dir.
b) İstanbul, Türkiye’nin başkenti olmadığı için q önermesinin doğruluk değeri 0 dır, yani q ≡ 0 dır.
c) “x = 5 ise x + 7 = 12 dir.” önermesi doğru bir önerme olduğu için, r ≡ 1 dir.
d) -1 sayısı en büyük negatif tam sayıdır. Dolayısıyla t önermesinin doğruluk değeri 0 dır, yani t ≡ 0 olur.
p ≡ r ≡ 1 ve q ≡ t ≡ 0 olduğundan p ile r, q ile t denk önermelerdir.

Bir Önermenin Değili (Olumsuzu)

Bir p önermesinin hükmünün olumsuzu alınarak elde edilen önermelere 0 önermenin değili (olumsuzu) denir. Bir önermenin değili p’ veya ~p sembolleriyle gösterilir.

1′ ≡ 0, 0′ ≡ 1 (1 in değili 0, 0 ın değili 1 dir.)
Bir önermenin değilinin değili kendisine denktir. (p’)’ ≡ p dir.

Örnek: p: “Bir saat 60 dakikadır”
önermesinin doğruluk değerini, önermenin değilini (olumsuzunu) ve değilinin doğruluk değerini belirtelim.

Çözüm: Bir saat 60 dakika olduğu için p ≡ 1 olur. p önermesinin değili (olumsuzu) p’: “Bir saat 60 dakika değildir.” önermesidir. Bu durumda p’ ≡ 0 olur.

BİLGİ:

Önermelerde Doğruluk Tabloları

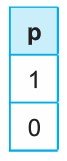
p önermesinin doğruluk değeri ya 1 ya da 0 olur. Dolayısıyla p önermesinin doğruluk tablosu aşağıdaki gibidir.

Birbirinden farklı p ile q önermelerinin, dört farklı doğruluk değeri vardır. Bunlar;
p doğru iken q doğru olabilir. p doğru iken q yanlış olabilir.
p yanlış iken q doğru olabilir. p yanlış iken q yanlış olabilir.
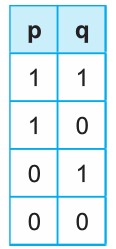
p ile q önermelerinin doğruluk tablosu ise aşağıdaki biçimde gösterilir.

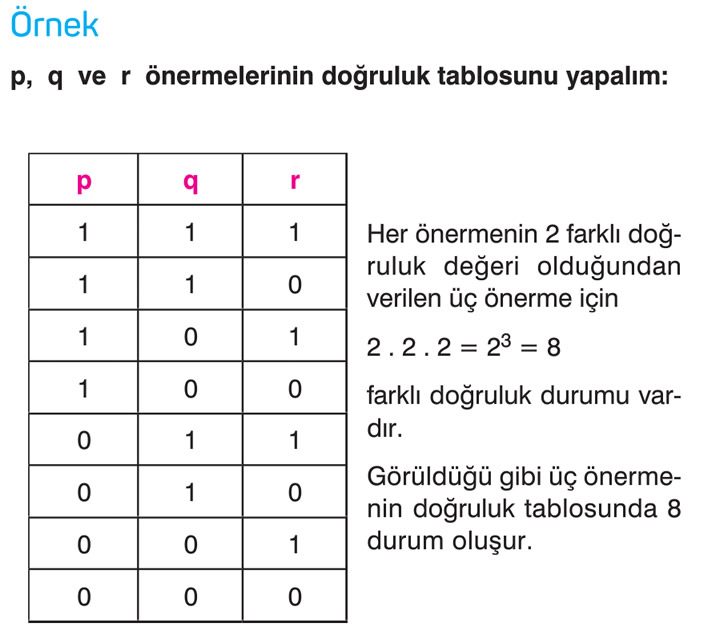
BİLGİ: n tane farklı önermenin, birlikte doğruluk değerleri için 2ⁿ tane farklı durum vardır.