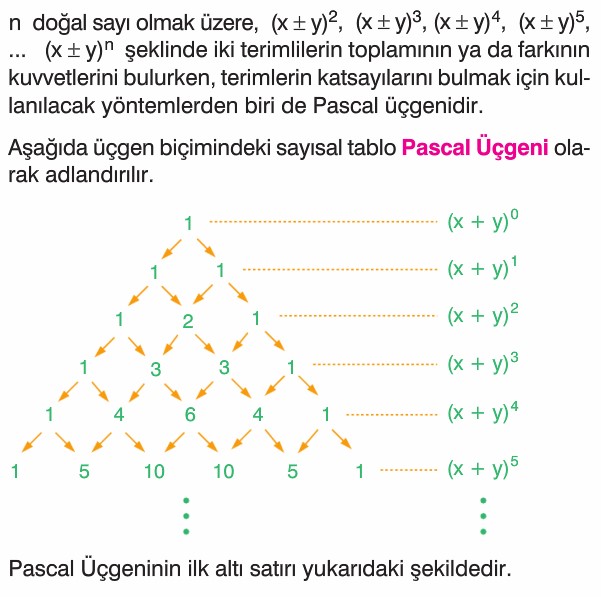
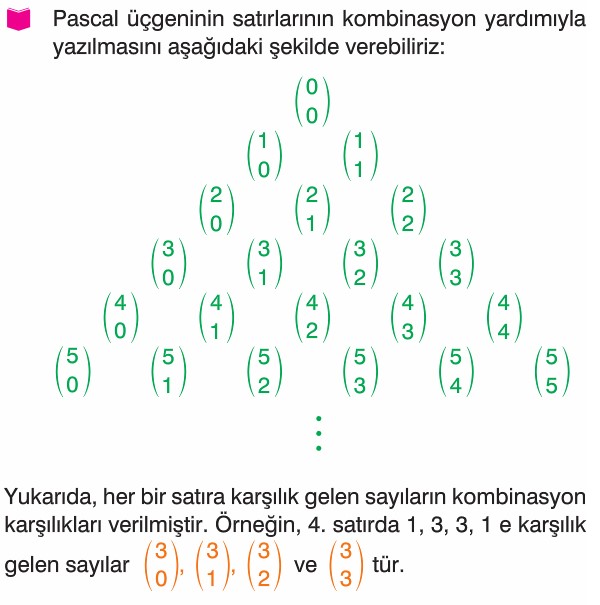
Pascal Üçgeni ve Binom Açılımı 10. Sınıf

Kategoriler: 10. Sınıf Matematik, Sayma ve Olasılık

Pascal Üçgeni

Pascal Üçgeni olarak isimlendirilen konu ve kavramlar Hint, Çin, İslam medeniyetlerindeki matematikçi ve düşünürler tarafından Pascal’dan çok önceleri ele alınmıştır. Pascal Üçgeni farklı medeniyetlerce biliniyordu. Hint medeniyetinde yaklaşık 5000 yıl önce dünyanın merkezinde olduğuna inanılan “Meru Dağı Merdiveni” adıyla, Çin medeniyetinde 11 . yüzyılda Çin’li matematikçi Jia Xian (1010-1070) tarafından,13. yüzyılda “Yang Hui Üçgeni” (1238 -1298) adıyla, İslam medeniyetinde “Ömer Hayyam Üçgeni” adıyla, Batı medeniyetinde ise günümüzde kullandığımız “Pascal Üçgeni” adıyla bilinmektedir. Bu şekilde matematiksel bilginin oluşumunda farklı kültür ve bilim insanlarının çok büyük rolü olmuştur.

Binom Açılımı

n doğal sayı olmak üzere, (x ± y)2, (x ± y)3, (x ± yy', (x ± y)5, (x ± y)n şeklinde iki terimlilerin toplamının ya da farkının kuvvetlerini bulurken, terimlerin katsayılarını bulmak için kullanılacak yöntemlerden biri de Pascal üçgenidir. Aşağıda üçgen biçimindeki sayısal tablo Pascal Üçgeni olarak adlandırılır.

Bir alt satırda ortada yer alan sayı bir üst satırdaki yan yana iki sayının toplamına eşittir. Pascal üçgeninin herhangi bir n. satırında, r. sırada bulunan sayı ile (r + 1). sırada bulunan sayının toplamı (n + 1). sıradaki (r + 1). sayıdır. Bu bağıntıya Pascal özdeşliği denir.
Örnek: Pascal üçgenin bazı satırlarının bir kısmı aşağıda verilmiştir. Buna göre, a + b + c + d nin değerini bulalım.
Çözüm: Özdeşliğe göre, a + b = 21 ve c + d = 35 tir. Buna güre, a + b + c+ d = 21 + 35 = 56 olur.

Sabit terim, değişkenlerden bağımsız terimdir. Bir açılımda sabit terimi bulmak için (eğer tanımlı ise) değişkenler yerine 0 yazılır. Bir açılımda katsayılar toplamını bulmak için değişkenler yerine 1 yazılır.

Örnek: (x -1)3 = x3 - 3x2 + 3x - 1 açılımında sabit terim -1 dir.  (x -1)3 = x3 - 3x2 + 3x -1 açılımında katsayılar toplamı, 1-3+3-1:0 dır.
Örnek: (3x + 2)7 ifadesinin açılımında, x = 0 İçin (3x+2)7 = (3+0+2)7 = 27 ise 128 olur. Buna göre, bu açılımda sabit terim 128 dir. x=1 için (3x+2)7 = (3+1+2)7 = 57 olur. Buna göre, bu açılımda katsayılar toplamı 57 dir.

Temel Yeterlilik Sınavı (TYT)
13 Haziran 2020 Cumartesi