SAYMA SAYILARI
Sayı saymak için kullanılan N+ = {1, 2, 3, 4, …} kümesinin elemanlarına sayma sayıları denir.
DOĞAL SAYILAR
Sayma sayılarına sıfır eklenerek elde edilen
N = {0, 1, 2, 3, 4, 5, … } kümesine doğal sayılar kümesi denir.
N = {0, 1, 2, 3, 4, 5, … } kümesinin her bir elemanına doğal sayı denir.
TAM SAYILAR KÜMESİ
Negatif tam sayıların doğal sayılara eklenmesiyle tam sayılar kümesi oluşur.
{ … ,-4, -3, -2, -1, 0, 1, 2, 3, 4, … } kümesine tam sayılar kümesi denir ve “Z” simgesiyle gösterilir.
Z = { …, -4, -3, -2, -1, 0, 1, 2, 3, 4, … } kümesinin her elemanına tam sayı denir.
Tam sayılar kümesinin negatif elemanlarından oluşan kümeye negatif tam sayılar kümesi denir ve “Z–” simgesiyle gösterilir.
Z– = { … , -5, -4, -3, -2, -1} Tam sayılar kümesinin pozitif elemanlarından oluşan kümeye pozitif tam sayılar kümesi denir ve Z+ ile gösterilir.
Z+ = {1, 2, 3, 4, 5, … }
Z = Z– ∪ {0} ∪ Z+
(Sıfır sayısı pozitif veya negatif değildir, işareti yoktur)
Her doğal sayı bir tam sayı olduğuna için N ⊂ Z dir.
Tek ve Çift Tam Sayılar
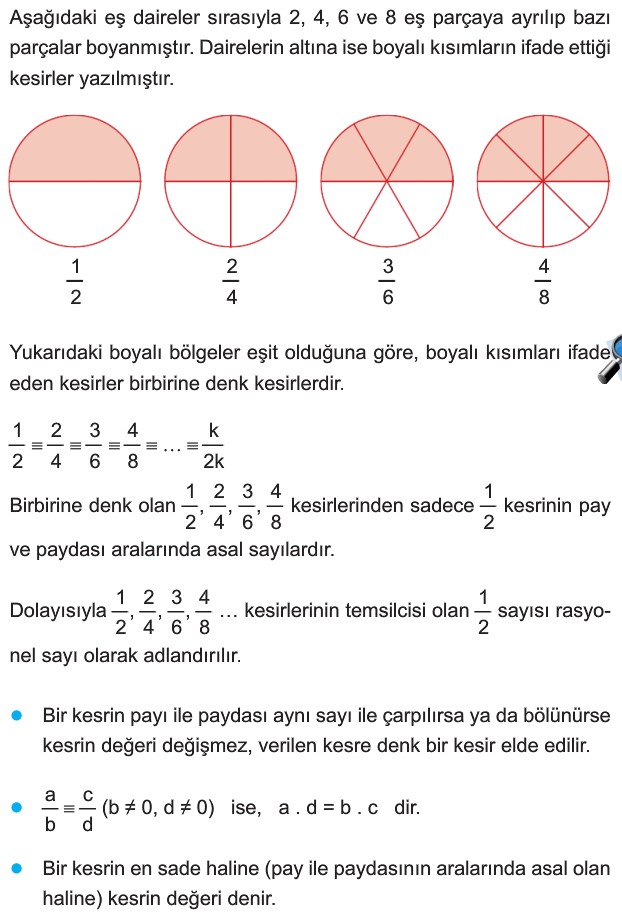
RASYONEL SAYILAR
Denk Kesirler
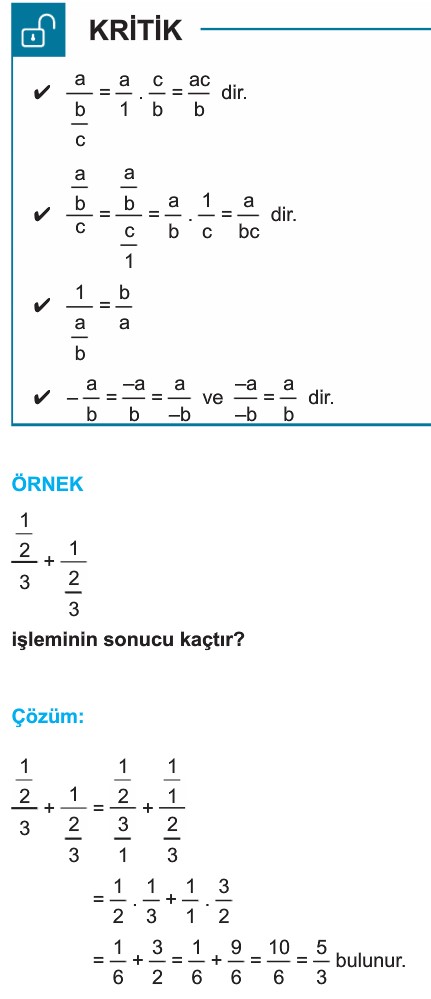
RASYONEL SAYILARDA İŞLEMLER
1. Toplama ve Çıkarma İşlemi
2. Çarpma İşlemi
3. Bölme İşlemi
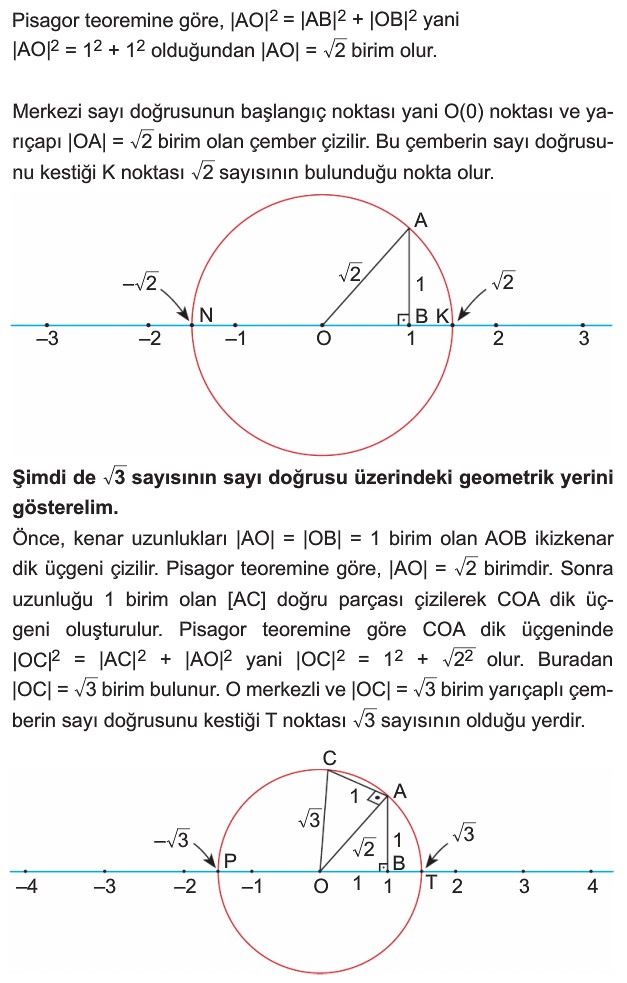
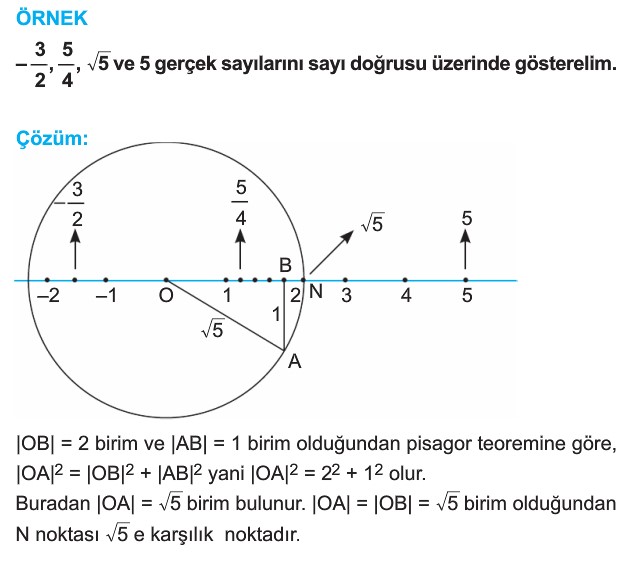
İRRASYONEL SAYILAR
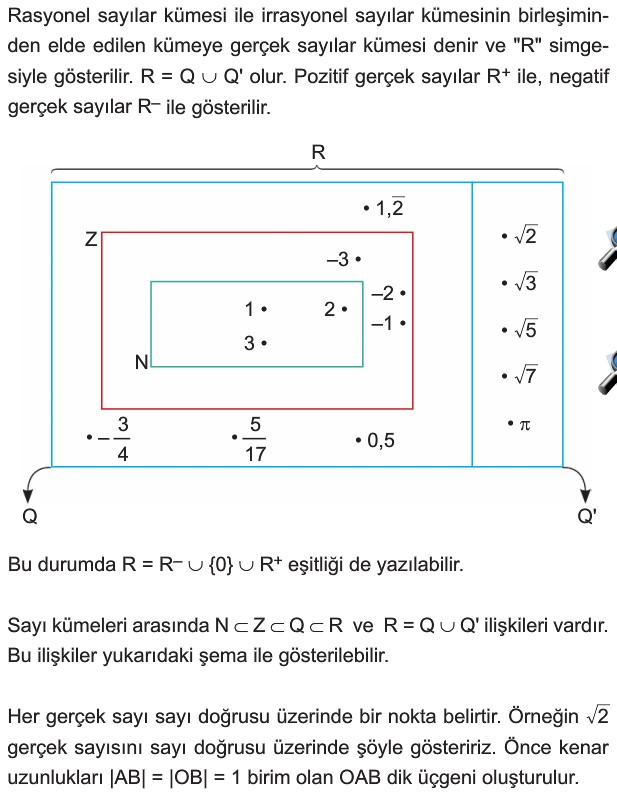
GERÇEK (REEL) SAYILAR
Gerçek Sayılar Kümesinde Toplama İşleminin Özellikleri
Gerçek Sayılar Kümesinde Çarpma İşleminin Özellikleri
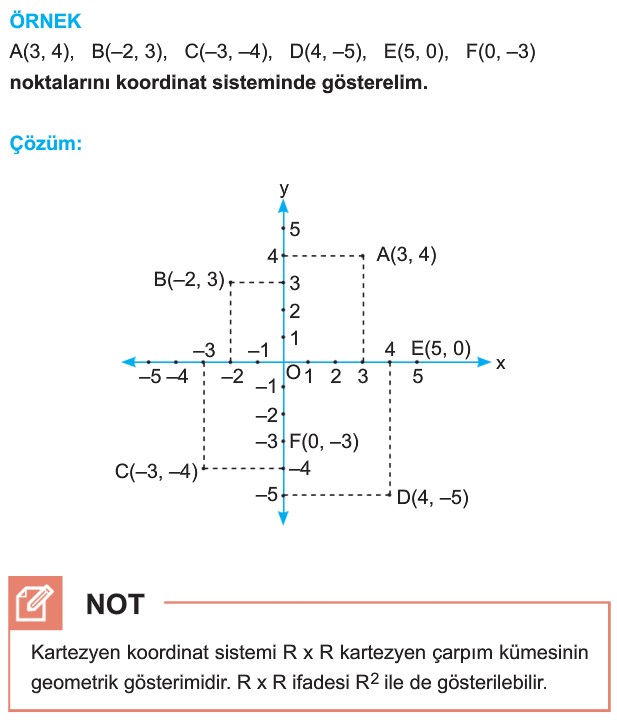
Kartezyen Koordinat Sistemi
Gerçek sayıların belirttiği her sıralı ikili, kartezyen koordinat sisteminde bir noktaya karşılık gelir. Koordinat sistemi, birbirine dik iki gerçek sayı doğrusunun sıfır noktasında kesişmesiyle elde edilmiştir. Bu kesişme noktası başlangıç noktası veya orijin olarak adlandırılır.